Somewhat Pointless: on the Existence or Emergence of Points in Euclid

“A point is that of which there is no part.”1
Can that which has no parts be truly said to exist? If so, in what way will that part-less thing be? Can that which has no part become part of another entity?
A point is a funny thing. It is the most infinitesimal of all geometric tools, yet they pop up in the most complex of geometric figures. It seems one cannot make a line without including at least two points,2 and we seem to pretend to understand them much better than we can readily explain.
But we can notice them; this seems to me the whole point.
Take Definition 3 as the first example: “[T]he extremities of a line are points.” If a point is something without parts, then it is ludicrous to suppose the line created is somehow an extension of two points reaching out to meet each other. This would introduce the property of extensibility into the points themselves, and to my mind requires a bit of something there that could be extended, drawn or produced between point A and point B. But points have no parts, and therefore cannot be extended. Lines are a different story: they have length, which is the necessary part to unlock this power of extensibility.3 I will endeavor to avoid talking about lines unless they interact with points themselves.
Returning to Definition 3, we know that the points cannot extend without parts, so the line must do that activity, and being “[L]ength without breadth” seems lacking in a certain regard. But we do notice something about this line: it has ends or extremities. At these ends we notice distinct points. It seems almost the most natural of activities to notice the ends of a thing. A young boy with a stick knows how to play swords with it, and knows the business end is the pointiest one. Give the same child a lollipop, and he knows which end is the business end, and which is the sad end. As with things physical, with lines these are the areas of attachment, of relation, and connection. From the end of a fishing-pole extends the line, and at the end of the line dangles the hook, and at the business end of the hook hangs the fish. The complete opposite end is held in our hand. We could call these things individually a locus for our focus. Though we interact with the rod, line, and fish as a whole, it seems done through interaction with parts.
And lines and figures act in a similar manner, drawing our focus to specific loci which we then name and likewise attach meaning. Even circles, which could contain multiple points, is defined by a solitary, central point from which the lines marking equidistance radiate toward the circumference of that same circle.4 “And the point is called the center of the circle.”5 This central focus allows the further division of the circle into specific properties and parts: the diameter,6 and the semicircle.7 It is not by happenstance that we notice the center of each of these parts and properties is the selfsame center point, helpfully named for us the center point.8 This locus is a pivotal seat of power when used correctly. It is a strong suggestion to relation: the circle does not live—geometrically-speaking—without it. And without it a circle cannot perform its most solemn task: directing our notice.
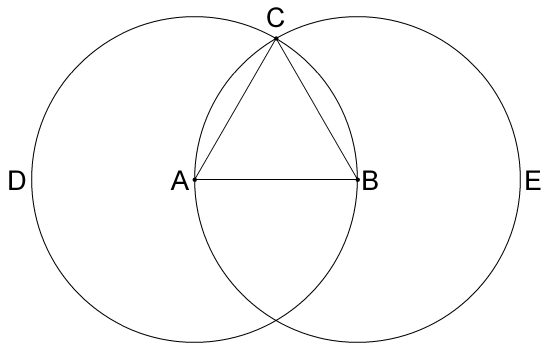
Take Proposition 1.
Only one straight line is given, and we are required to construct an equilateral triangle. We notice that said straight line has end-points and they are named A and B respectively for us. The astute student will notice that we effectively have, in one sense, two-thirds of a triangle, since upon noticing a third point will we be able to construct sides9 and complete our project. Effectively we only lack a third point, which for ease we will call C, and currently lack the means to notice its possible location. Here circles D and E prove invaluable. When constructed with AB as their respective radius they give two possible points, two possible loci, toward which we focus our attention and likewise the sides for a triangle. This point C shows us three relations:
1. One of two points at which circles D and B cross and cut each other.
2. One of two possibilities for a relation of lines equal to AB, being itself on the circumference of D and E at once and those created lines AC and BC being radii.
3. Once connected through Postulate 1 it shows the relation had in radii of intersecting circles and their capacity for creation of figures, here an equilateral triangle.
Without circles located with their midpoints on A and B respectively, we have little hope of having a locus for our focus, be that in completion of what was required or the highlighting of possible relations. And without this locus we have no hope of using Postulate 1 to complete our task; we have no point toward which we extend our lines AC and BC. Happily the circles direct our focus to possibilities created by their intersections, these points of focus.
This focus at intersection proves itself most dramatically in Proposition 3.
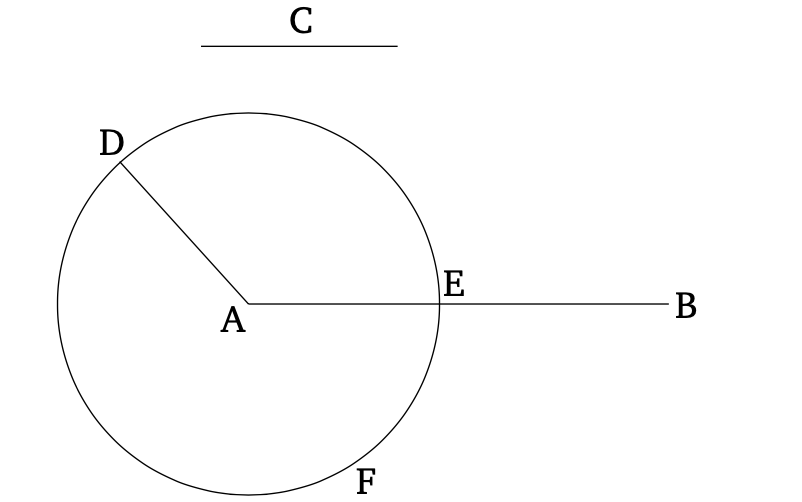
The annunciation reads: “For two given unequal straight lines, to cut off from the greater a straight line equal to the lesser.” And we’ll see right off there is something strange about one of these lines.
The first, called AB, is fairly standard as a line: it’s straight and it has two endpoints. The second line is indeed straight, but has no distinct endpoints. This one fact prevents us from directly comparing the second line with the first; we are unable to focus on this direct comparison. Therefore, we turn to other tools to help draw our attention and create loci toward which we may focus and thereby relate our two disparate lines.
Much like Proposition 1, circles are key in allowing us to glimpse the points which allow for relation. If we were to move through steps available to us through Propositions 1 and 2, we see a kaleidoscope of circles, lines, triangles, and by relation points which allow us to draw a line on point A to point D, creating line AD, which by Proposition 2 is equal to our “pointless” line C. We thus have wherewith to relate our longer line AB with our given, relation-less line C. Using A as the center point of a circle F, and AD as its radius, we can then highlight a new point E on AB equal to C on the intersection of Circle F and Line AB. And then the circle cuts line AB at point E, creating another, slightly obscured relation. AE and AD are related in length because of their relation to A as a center point, thus establishing both as radii of circle F.
Without the relation of distinct endpoints on which to focus our attention it proves impossible to compare lines AB and C unless we have more points upon which to focus, or to serve as loci for our notice. This pointless line is not meant to suggest the line C in Proposition 3 does not have points that could possibly appear on it, nor that it does not have endpoints. The interesting thing here is we seem, by Euclid’s design, to be limited in our viewing them or perhaps they are purposefully obscured through geometric legerdemain such that we cannot say: “Look, C is of such-and-such length, let us pick it up and use it as our measure.” We need points to do that.
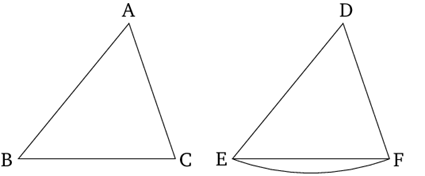
We are told to do just so in the following Proposition 4. The neat thing about a triangle is not only is it defined by its sides and its angles,10 if those sides meeting at those angles happen to do so at their ends, then we have points.11 And even if that is not the case, it has been shown in the preceding Propositions that points are signaled by circles that cut and lines that then meet. Ultimately the only triangle we can surely create from Proposition 1 is an equilateral triangle, anyway, but given any two triangles we can take and place their corresponding points one-on-top-of-the-other to compare. “For if triangle ABC is applied to triangle DEF, the point A being placed on the point D, and the straight-line AB on DE, then the point B will also coincide with [the point] E, on account of AB being equal to DE.”12
That which we could not do with Proposition 3’s C we could do with a complete triangle, and the points are the motor here. They are the attachments, and they are that which we first relate between the two triangles ABC and DEF: A to D, B to E, C to F, and so on. They are the first loci we notice, and they are in fact the names of the triangles. And with those relations firmly fixed in our minds we are enabled to then move around whole triangles with their attendant lines.
But if points have no part, can they coincide? In the proposition above Common Notion 4 becomes quite important: “[T]hings coinciding with one another are equal to one another.” Are points things? Can we rightly call them an entity? My suspicion is this wording is a mistake of translation and so I choose not to take it too seriously. So I answer that what better than something of dubious existence to then take up the same “place” in our notice than that which has no part? If space is not an attribute of a point, then it seems not improbable that two or more could share it. We can hold at least two things (being an operative word) in our focus at once to then compare or superimpose one triangle from Proposition 4 to the other by way of their orienting and relating points.
These loci signaled by their attendant points do much work over the course of Book I, drawing attention to increasingly complex relations, proofs, and contradictions. Eventually Euclid leaves off highlighting a point’s presence to the student, but still they beckon the geometric eye, that focus, to notice the in the figures presented a constellation of interlocking interest.
Perhaps points reveal themselves, and we can only notice them as they do.
Endnotes:
1 Unless otherwise stated, all citations come from Euclid’s Elements, Book 1. Here we cite Definition 1.
2 Definitions 3 & 4
3 Postulates 1 & 2
4 Definition 15
5 Definition 16
6 Definition 17
7 Definition 18
8 ibid.
9 This given us a power as part of Postulate 1. This would seem to cause issues as we have power “to draw a straight line from any point to any point,” but let us remember two things:
1. Points are not being extended, it is the line that is extended to connect.
2. Points are not taken at random from the space of a plane. This will be treated more in-depth later.
10 Definitions 20 & 21
11 Definition 3
12 Proposition 4, emphasis added